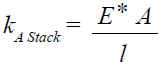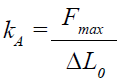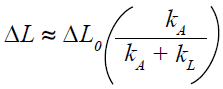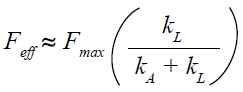プリロードと荷重容量
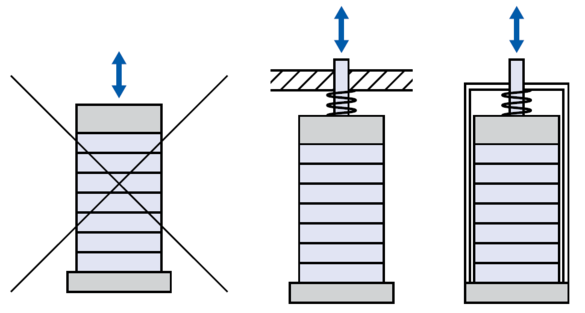
壊れやすい圧電アクチュエータおよび単結晶アクチュエータの引張強度は、5~10 MPaと比較的小さい値となります。このため、装置ではアクチュエータに対し力学的なプリロードをかけることが推奨されます。プリロードはできる限り小さいものを選ぶ必要があります。経験によれば>>動的外力の補償には15 MPaで十分であり、荷重が一定の場合30 MPaを超えないようにする必要があります。
横方向の力は、短いアクチュエータでは主として剪断応力を発生させます。縦横比の大きい長いアクチュエータでは、さらに曲げ応力が生じます。2つの荷重を合わせたものが横方向の最大荷重容量であり>> PICA剪断アクチュエータのものがデータシートに記載されています。これらの値は、寸法が近いアクチュエータでも流用できます。ただし、通常は、ガイドを使用して横方向の力からアクチュエータを保護することが推奨されます。
プリロードの制限
アクチュエータは、数十MPaですでに力学的に消極し始めます。大信号制御を行うとアクチュエータは再度分極します。この制御を行うと、一方では生じる変位が増大しますが、また一方では有効容量および損失が増加し、コンポーネントの寿命に悪影響が生じます。
また、圧力によるプリロードでも、> 引張応力がある程度生じます。このため、非常に大きいプリロードを使用する場合、局所的に引張強度を上回る可能性があります。使用可能なプリロードの大きさは、セラミック素材の強度では決まりません。ピエゾアクチュエータでは、250 MPaを超える圧縮強度が得られます。
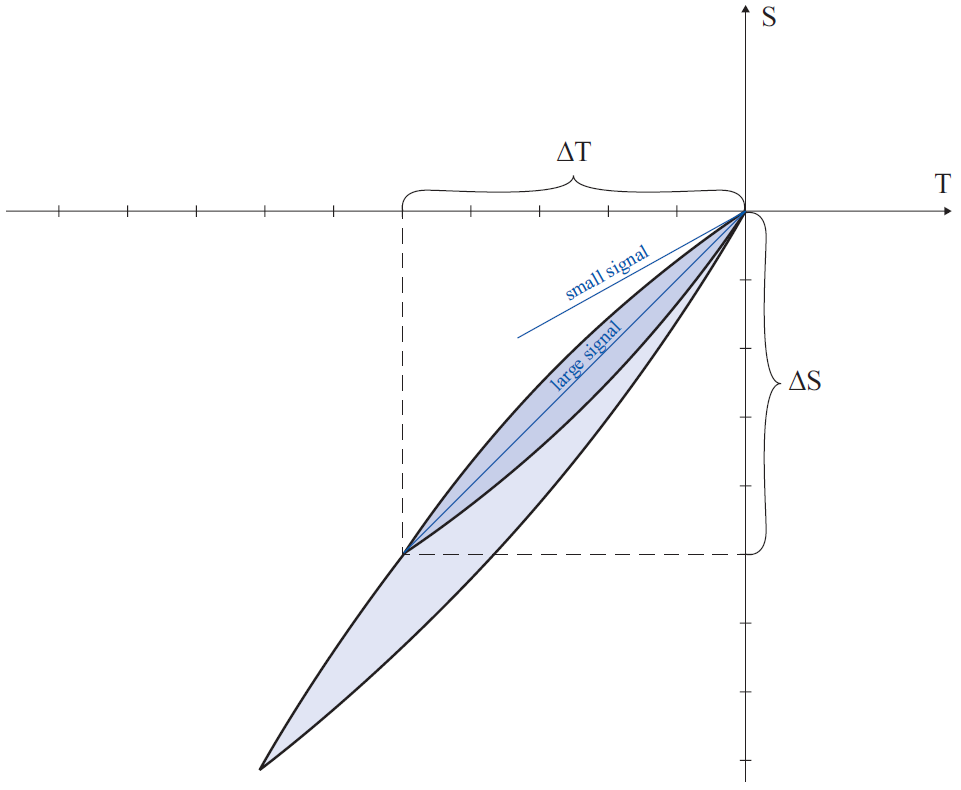
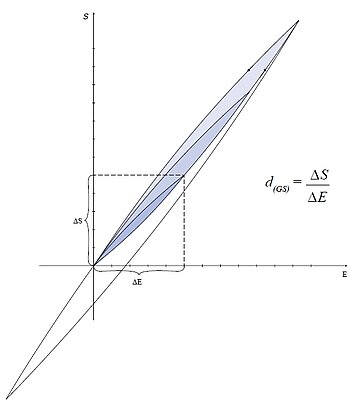
ピエゾアクチュエータを指定する場合、準静的な大信号剛性は電界強度または電圧が大きく力学的プリロードが小さい同時制御で決まります。この剛性は好ましくない動作事例を考慮に入れる際に役立ちます。すなわち、多くの用途では実際のアクチュエータの剛性は大きいものになります。
PICAアクチュエータには接着層がありますが、剛性はわずかしか減少しません。最適化した技術を用いることで接着剤の隙間は数マイクロメートル程度の高さに抑えられているため、大信号剛性は、接着層の多層アクチュエータからわずか10~20 %程度小さいものとなります。対向面に対する比較的柔軟な接点を有する球状の末端部など、全体の剛性にはアクチュエータの設計がはるかに大きい影響を及ぼします。
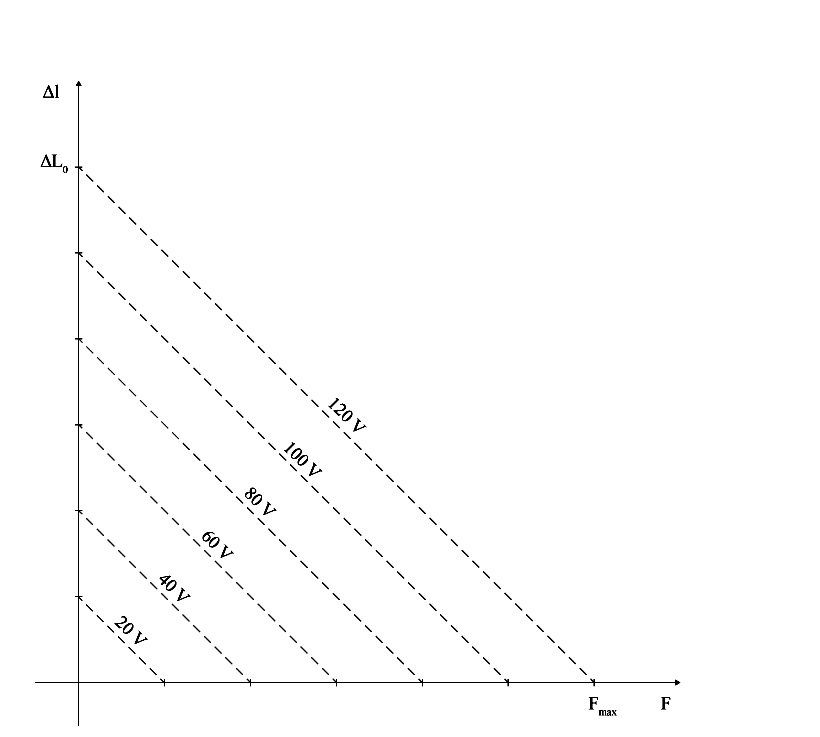
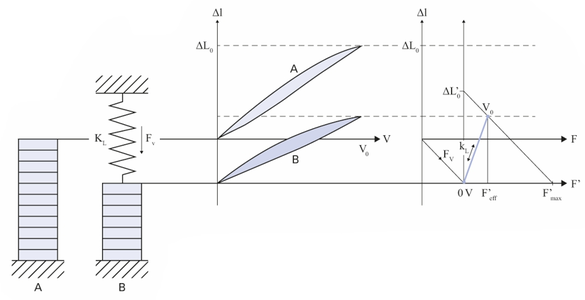
縦方向積層アクチュエータでは、アクチュエータの長さが変位ΔL0の決定変数になります。2 kV/mmの公称電界強度では、長さの0.10~0.15 %の変位を達成可能です。発生力Fmaxは断面積で決まります。このアクチュエータでは、30 N/mm²程度を実現可能です。
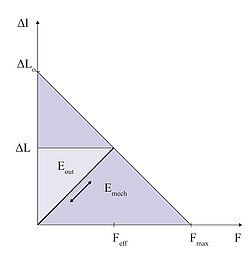
したがって、達成すべき力学的エネルギーEmech = (Δ L0 Fmax)/2の決定パラメーターはアクチュエータの体積になります。
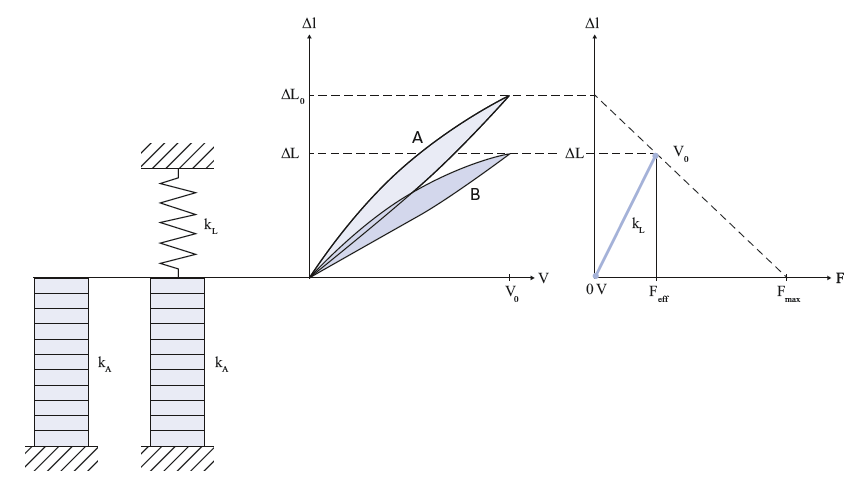
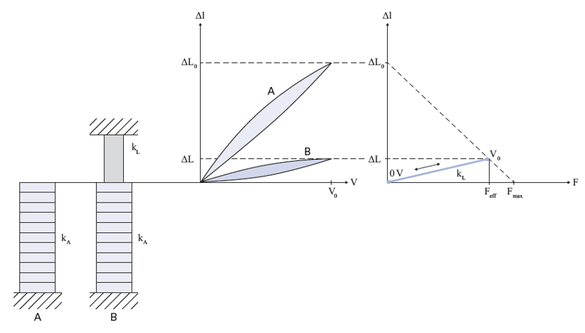
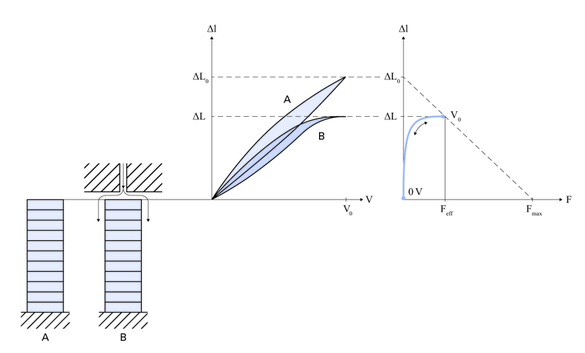
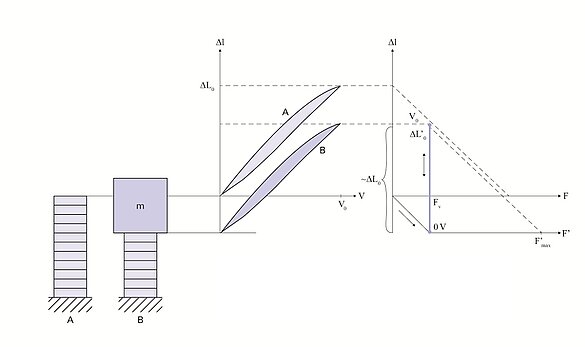
アクチュエータの動作時に電気エネルギーから力学的エネルギーへと変換されるエネルギー量E mechは、図9の曲線下の面積に相当します。ただし、力学的負荷に伝達できるのはこの総量の一部分のEout のみです。力学系は、曲線下の面積が最大となる場合にエネルギー的に最適となります。これは、負荷の剛性とアクチュエータの剛性が等しい場合に生じます。動作グラフでは、薄い青色部分の面積がこのエネルギー量に相当します。縦方向ピエゾアクチュエータでは2~5 mJ/cm³程度の力学的仕事を行うことができ、ベンディングアクチュエータで達成できる仕事量はこの10分の1程度となります。